Pylab - Matlab style Python¶
Pylab is a module that provides a Matlab like namespace by importing functions from the modules Numpy and Matplotlib. Numpy provides efficient numerical vector calculations based on underlying Fortran and C binary libraries. Matplotlib contains functions to create visualizations of data.
# this ipython magic command imports pylab and allows the plots to reside within the notebook
%pylab inline
Populating the interactive namespace from numpy and matplotlib
Value error parsing header in AFM: b'UnderlinePosition' b'-133rUnderlineThickness 20rVersion 7.000'
The following examples are based on Florian Lhuillier’s lecture on Matlab which can be found online:
http://geophysik.uni-muenchen.de/~lhuillier/teaching/AD2010/
Examples based on “Rappels d’utilisation de MATLAB”¶
numpy.array¶
M = array(((1,2,3), (4,5,6), (7,8,9)))
M
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
L=array((1,2,3))
C=array((1,2,3)).T
L, C
(array([1, 2, 3]), array([1, 2, 3]))
t1=arange(1,11); t1
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
t2=arange(1,11,2); t2
array([1, 3, 5, 7, 9])
t3=arange(10,0,-1); t3
array([10, 9, 8, 7, 6, 5, 4, 3, 2, 1])
get specific elements¶
t1
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
t1[4]
5
t1[[0,4,9]]
array([ 1, 5, 10])
t1[0:5]
array([1, 2, 3, 4, 5])
t1[0::2]
array([1, 3, 5, 7, 9])
t1[1::2]
array([ 2, 4, 6, 8, 10])
t1>5
array([False, False, False, False, False, True, True, True, True, True], dtype=bool)
t1[t1>5]
array([ 6, 7, 8, 9, 10])
t1%2==0
array([False, True, False, True, False, True, False, True, False, True], dtype=bool)
t1[t1%2==0]
array([ 2, 4, 6, 8, 10])
t1%2==1
array([ True, False, True, False, True, False, True, False, True, False], dtype=bool)
t1[t1%2==1]
array([1, 3, 5, 7, 9])
Matplotlib plotting¶
t = arange( -2*pi,2*pi,0.1); t
array([-6.28318531, -6.18318531, -6.08318531, -5.98318531, -5.88318531,
-5.78318531, -5.68318531, -5.58318531, -5.48318531, -5.38318531,
-5.28318531, -5.18318531, -5.08318531, -4.98318531, -4.88318531,
-4.78318531, -4.68318531, -4.58318531, -4.48318531, -4.38318531,
-4.28318531, -4.18318531, -4.08318531, -3.98318531, -3.88318531,
-3.78318531, -3.68318531, -3.58318531, -3.48318531, -3.38318531,
-3.28318531, -3.18318531, -3.08318531, -2.98318531, -2.88318531,
-2.78318531, -2.68318531, -2.58318531, -2.48318531, -2.38318531,
-2.28318531, -2.18318531, -2.08318531, -1.98318531, -1.88318531,
-1.78318531, -1.68318531, -1.58318531, -1.48318531, -1.38318531,
-1.28318531, -1.18318531, -1.08318531, -0.98318531, -0.88318531,
-0.78318531, -0.68318531, -0.58318531, -0.48318531, -0.38318531,
-0.28318531, -0.18318531, -0.08318531, 0.01681469, 0.11681469,
0.21681469, 0.31681469, 0.41681469, 0.51681469, 0.61681469,
0.71681469, 0.81681469, 0.91681469, 1.01681469, 1.11681469,
1.21681469, 1.31681469, 1.41681469, 1.51681469, 1.61681469,
1.71681469, 1.81681469, 1.91681469, 2.01681469, 2.11681469,
2.21681469, 2.31681469, 2.41681469, 2.51681469, 2.61681469,
2.71681469, 2.81681469, 2.91681469, 3.01681469, 3.11681469,
3.21681469, 3.31681469, 3.41681469, 3.51681469, 3.61681469,
3.71681469, 3.81681469, 3.91681469, 4.01681469, 4.11681469,
4.21681469, 4.31681469, 4.41681469, 4.51681469, 4.61681469,
4.71681469, 4.81681469, 4.91681469, 5.01681469, 5.11681469,
5.21681469, 5.31681469, 5.41681469, 5.51681469, 5.61681469,
5.71681469, 5.81681469, 5.91681469, 6.01681469, 6.11681469,
6.21681469])
x1=cos(t)
x2=sin(t)
len(x2)
126
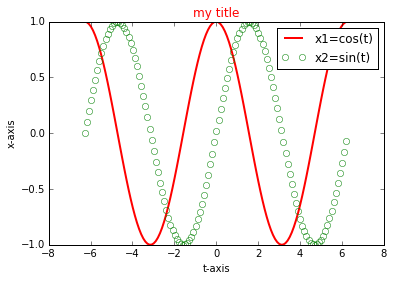
plot(t,x1, color='r', linewidth=2, label='x1=cos(t)')
plot(t, x2, ' o', markeredgecolor='g', markerfacecolor="None", label='x2=sin(t)')
title('my title', color='r')
xlabel('t-axis')
ylabel('x-axis')
legend()
<matplotlib.legend.Legend at 0x7f5fe9c0dc18>
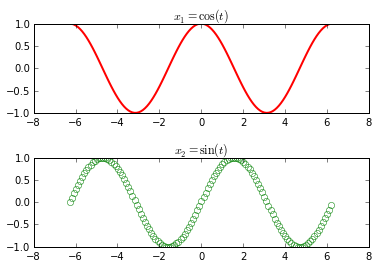
subplot(211)
plot(t, x1, 'r', linewidth=2)
title('$x_1=\cos(t)$')
subplot(212)
plot(t, x2, ' o', markeredgecolor='g', markerfacecolor="None")
title('$x_2=\sin(t)$')
subplots_adjust(hspace=.5)
Examples based on “familiarisation avec Matlab”¶
set_printoptions(precision=2, suppress=True)
Excercise 1¶
x=array((17,8,12,15,6,11,9,18,16,10,13,19)); x
array([17, 8, 12, 15, 6, 11, 9, 18, 16, 10, 13, 19])
N = len(x); N
12
S = sum(x); S
154
xbarre = S / N; xbarre
12.833333333333334
xbarre = mean( x); xbarre
12.833333333333334
sigma = sqrt(sum((x-xbarre)**2)/(N-1)); sigma
4.1959576506514704
sigma = std(x, ddof=1); sigma
4.1959576506514704
dx = x[1:]-x[0:-1]; dx
array([-9, 4, 3, -9, 5, -2, 9, -2, -6, 3, 6])
dx = diff(x); dx
array([-9, 4, 3, -9, 5, -2, 9, -2, -6, 3, 6])
Excercise 2¶
t = linspace(-25,25,51); t
array([-25., -24., -23., -22., -21., -20., -19., -18., -17., -16., -15.,
-14., -13., -12., -11., -10., -9., -8., -7., -6., -5., -4.,
-3., -2., -1., 0., 1., 2., 3., 4., 5., 6., 7.,
8., 9., 10., 11., 12., 13., 14., 15., 16., 17., 18.,
19., 20., 21., 22., 23., 24., 25.])
x = t**2; x
array([ 625., 576., 529., 484., 441., 400., 361., 324., 289.,
256., 225., 196., 169., 144., 121., 100., 81., 64.,
49., 36., 25., 16., 9., 4., 1., 0., 1.,
4., 9., 16., 25., 36., 49., 64., 81., 100.,
121., 144., 169., 196., 225., 256., 289., 324., 361.,
400., 441., 484., 529., 576., 625.])
y = t[::-1]**3; y
array([ 15625., 13824., 12167., 10648., 9261., 8000., 6859.,
5832., 4913., 4096., 3375., 2744., 2197., 1728.,
1331., 1000., 729., 512., 343., 216., 125.,
64., 27., 8., 1., 0., -1., -8.,
-27., -64., -125., -216., -343., -512., -729.,
-1000., -1331., -1728., -2197., -2744., -3375., -4096.,
-4913., -5832., -6859., -8000., -9261., -10648., -12167.,
-13824., -15625.])
fliplr(t[newaxis])**3
array([[ 15625., 13824., 12167., 10648., 9261., 8000., 6859.,
5832., 4913., 4096., 3375., 2744., 2197., 1728.,
1331., 1000., 729., 512., 343., 216., 125.,
64., 27., 8., 1., 0., -1., -8.,
-27., -64., -125., -216., -343., -512., -729.,
-1000., -1331., -1728., -2197., -2744., -3375., -4096.,
-4913., -5832., -6859., -8000., -9261., -10648., -12167.,
-13824., -15625.]])
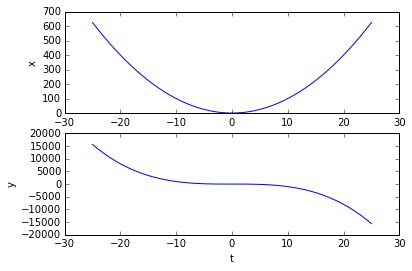
subplot(2,1,1)
plot(t,x)
xlabel('t'); ylabel('x')
subplot(212)
plot(t,y)
xlabel('t'); ylabel('y')
<matplotlib.text.Text at 0x7f5fe95ac978>
fix(x/2)==x/2
array([False, True, False, True, False, True, False, True, False,
True, False, True, False, True, False, True, False, True,
False, True, False, True, False, True, False, True, False,
True, False, True, False, True, False, True, False, True,
False, True, False, True, False, True, False, True, False,
True, False, True, False, True, False], dtype=bool)
sum( x[fix(x/2)==x/2])
5200.0
sum( x[remainder(x,2)==0])
5200.0
sum( x[x%2==0])
5200.0
sum( y[y>0])
105625.0
Excercise 3¶
t = arange(1,10.01,0.5); t
array([ 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. ,
5.5, 6. , 6.5, 7. , 7.5, 8. , 8.5, 9. , 9.5, 10. ])
A = array( (t, t**2, t**3, t**4)).T; A
array([[ 1. , 1. , 1. , 1. ],
[ 1.5 , 2.25, 3.38, 5.06],
[ 2. , 4. , 8. , 16. ],
[ 2.5 , 6.25, 15.62, 39.06],
[ 3. , 9. , 27. , 81. ],
[ 3.5 , 12.25, 42.88, 150.06],
[ 4. , 16. , 64. , 256. ],
[ 4.5 , 20.25, 91.12, 410.06],
[ 5. , 25. , 125. , 625. ],
[ 5.5 , 30.25, 166.38, 915.06],
[ 6. , 36. , 216. , 1296. ],
[ 6.5 , 42.25, 274.62, 1785.06],
[ 7. , 49. , 343. , 2401. ],
[ 7.5 , 56.25, 421.88, 3164.06],
[ 8. , 64. , 512. , 4096. ],
[ 8.5 , 72.25, 614.12, 5220.06],
[ 9. , 81. , 729. , 6561. ],
[ 9.5 , 90.25, 857.38, 8145.06],
[ 10. , 100. , 1000. , 10000. ]])
A = column_stack((A, t>5)); A
array([[ 1. , 1. , 1. , 1. , 0. ],
[ 1.5 , 2.25, 3.38, 5.06, 0. ],
[ 2. , 4. , 8. , 16. , 0. ],
[ 2.5 , 6.25, 15.62, 39.06, 0. ],
[ 3. , 9. , 27. , 81. , 0. ],
[ 3.5 , 12.25, 42.88, 150.06, 0. ],
[ 4. , 16. , 64. , 256. , 0. ],
[ 4.5 , 20.25, 91.12, 410.06, 0. ],
[ 5. , 25. , 125. , 625. , 0. ],
[ 5.5 , 30.25, 166.38, 915.06, 1. ],
[ 6. , 36. , 216. , 1296. , 1. ],
[ 6.5 , 42.25, 274.62, 1785.06, 1. ],
[ 7. , 49. , 343. , 2401. , 1. ],
[ 7.5 , 56.25, 421.88, 3164.06, 1. ],
[ 8. , 64. , 512. , 4096. , 1. ],
[ 8.5 , 72.25, 614.12, 5220.06, 1. ],
[ 9. , 81. , 729. , 6561. , 1. ],
[ 9.5 , 90.25, 857.38, 8145.06, 1. ],
[ 10. , 100. , 1000. , 10000. , 1. ]])
column_stack((A, (fix(t)==t)*5))
array([[ 1. , 1. , 1. , 1. , 0. , 5. ],
[ 1.5 , 2.25, 3.38, 5.06, 0. , 0. ],
[ 2. , 4. , 8. , 16. , 0. , 5. ],
[ 2.5 , 6.25, 15.62, 39.06, 0. , 0. ],
[ 3. , 9. , 27. , 81. , 0. , 5. ],
[ 3.5 , 12.25, 42.88, 150.06, 0. , 0. ],
[ 4. , 16. , 64. , 256. , 0. , 5. ],
[ 4.5 , 20.25, 91.12, 410.06, 0. , 0. ],
[ 5. , 25. , 125. , 625. , 0. , 5. ],
[ 5.5 , 30.25, 166.38, 915.06, 1. , 0. ],
[ 6. , 36. , 216. , 1296. , 1. , 5. ],
[ 6.5 , 42.25, 274.62, 1785.06, 1. , 0. ],
[ 7. , 49. , 343. , 2401. , 1. , 5. ],
[ 7.5 , 56.25, 421.88, 3164.06, 1. , 0. ],
[ 8. , 64. , 512. , 4096. , 1. , 5. ],
[ 8.5 , 72.25, 614.12, 5220.06, 1. , 0. ],
[ 9. , 81. , 729. , 6561. , 1. , 5. ],
[ 9.5 , 90.25, 857.38, 8145.06, 1. , 0. ],
[ 10. , 100. , 1000. , 10000. , 1. , 5. ]])
column_stack((A, (remainder(t,1)==0)*5))
array([[ 1. , 1. , 1. , 1. , 0. , 5. ],
[ 1.5 , 2.25, 3.38, 5.06, 0. , 0. ],
[ 2. , 4. , 8. , 16. , 0. , 5. ],
[ 2.5 , 6.25, 15.62, 39.06, 0. , 0. ],
[ 3. , 9. , 27. , 81. , 0. , 5. ],
[ 3.5 , 12.25, 42.88, 150.06, 0. , 0. ],
[ 4. , 16. , 64. , 256. , 0. , 5. ],
[ 4.5 , 20.25, 91.12, 410.06, 0. , 0. ],
[ 5. , 25. , 125. , 625. , 0. , 5. ],
[ 5.5 , 30.25, 166.38, 915.06, 1. , 0. ],
[ 6. , 36. , 216. , 1296. , 1. , 5. ],
[ 6.5 , 42.25, 274.62, 1785.06, 1. , 0. ],
[ 7. , 49. , 343. , 2401. , 1. , 5. ],
[ 7.5 , 56.25, 421.88, 3164.06, 1. , 0. ],
[ 8. , 64. , 512. , 4096. , 1. , 5. ],
[ 8.5 , 72.25, 614.12, 5220.06, 1. , 0. ],
[ 9. , 81. , 729. , 6561. , 1. , 5. ],
[ 9.5 , 90.25, 857.38, 8145.06, 1. , 0. ],
[ 10. , 100. , 1000. , 10000. , 1. , 5. ]])
column_stack((A, (mod(t,1)==0)*5))
array([[ 1. , 1. , 1. , 1. , 0. , 5. ],
[ 1.5 , 2.25, 3.38, 5.06, 0. , 0. ],
[ 2. , 4. , 8. , 16. , 0. , 5. ],
[ 2.5 , 6.25, 15.62, 39.06, 0. , 0. ],
[ 3. , 9. , 27. , 81. , 0. , 5. ],
[ 3.5 , 12.25, 42.88, 150.06, 0. , 0. ],
[ 4. , 16. , 64. , 256. , 0. , 5. ],
[ 4.5 , 20.25, 91.12, 410.06, 0. , 0. ],
[ 5. , 25. , 125. , 625. , 0. , 5. ],
[ 5.5 , 30.25, 166.38, 915.06, 1. , 0. ],
[ 6. , 36. , 216. , 1296. , 1. , 5. ],
[ 6.5 , 42.25, 274.62, 1785.06, 1. , 0. ],
[ 7. , 49. , 343. , 2401. , 1. , 5. ],
[ 7.5 , 56.25, 421.88, 3164.06, 1. , 0. ],
[ 8. , 64. , 512. , 4096. , 1. , 5. ],
[ 8.5 , 72.25, 614.12, 5220.06, 1. , 0. ],
[ 9. , 81. , 729. , 6561. , 1. , 5. ],
[ 9.5 , 90.25, 857.38, 8145.06, 1. , 0. ],
[ 10. , 100. , 1000. , 10000. , 1. , 5. ]])
column_stack((A, (t % 1==0)*5))
array([[ 1. , 1. , 1. , 1. , 0. , 5. ],
[ 1.5 , 2.25, 3.38, 5.06, 0. , 0. ],
[ 2. , 4. , 8. , 16. , 0. , 5. ],
[ 2.5 , 6.25, 15.62, 39.06, 0. , 0. ],
[ 3. , 9. , 27. , 81. , 0. , 5. ],
[ 3.5 , 12.25, 42.88, 150.06, 0. , 0. ],
[ 4. , 16. , 64. , 256. , 0. , 5. ],
[ 4.5 , 20.25, 91.12, 410.06, 0. , 0. ],
[ 5. , 25. , 125. , 625. , 0. , 5. ],
[ 5.5 , 30.25, 166.38, 915.06, 1. , 0. ],
[ 6. , 36. , 216. , 1296. , 1. , 5. ],
[ 6.5 , 42.25, 274.62, 1785.06, 1. , 0. ],
[ 7. , 49. , 343. , 2401. , 1. , 5. ],
[ 7.5 , 56.25, 421.88, 3164.06, 1. , 0. ],
[ 8. , 64. , 512. , 4096. , 1. , 5. ],
[ 8.5 , 72.25, 614.12, 5220.06, 1. , 0. ],
[ 9. , 81. , 729. , 6561. , 1. , 5. ],
[ 9.5 , 90.25, 857.38, 8145.06, 1. , 0. ],
[ 10. , 100. , 1000. , 10000. , 1. , 5. ]])
column_stack((A, (A[:,1] % 1==0)*5))
array([[ 1. , 1. , 1. , 1. , 0. , 5. ],
[ 1.5 , 2.25, 3.38, 5.06, 0. , 0. ],
[ 2. , 4. , 8. , 16. , 0. , 5. ],
[ 2.5 , 6.25, 15.62, 39.06, 0. , 0. ],
[ 3. , 9. , 27. , 81. , 0. , 5. ],
[ 3.5 , 12.25, 42.88, 150.06, 0. , 0. ],
[ 4. , 16. , 64. , 256. , 0. , 5. ],
[ 4.5 , 20.25, 91.12, 410.06, 0. , 0. ],
[ 5. , 25. , 125. , 625. , 0. , 5. ],
[ 5.5 , 30.25, 166.38, 915.06, 1. , 0. ],
[ 6. , 36. , 216. , 1296. , 1. , 5. ],
[ 6.5 , 42.25, 274.62, 1785.06, 1. , 0. ],
[ 7. , 49. , 343. , 2401. , 1. , 5. ],
[ 7.5 , 56.25, 421.88, 3164.06, 1. , 0. ],
[ 8. , 64. , 512. , 4096. , 1. , 5. ],
[ 8.5 , 72.25, 614.12, 5220.06, 1. , 0. ],
[ 9. , 81. , 729. , 6561. , 1. , 5. ],
[ 9.5 , 90.25, 857.38, 8145.06, 1. , 0. ],
[ 10. , 100. , 1000. , 10000. , 1. , 5. ]])
Excercise 4¶
def matrace(A):
if A.shape[0] == A.shape[1]: # square matrix
return sum(A.diagonal())
else:
return -1
B = randn(10,2); B
array([[ 0.63495405, -0.41332203],
[-0.7815181 , -0.13233533],
[ 0.7135537 , -2.28650789],
[ 1.06424592, -0.59932232],
[-0.92327638, 1.08949032],
[-0.3044619 , -1.41034731],
[ 2.43510089, 1.79379768],
[ 1.72210238, -0.07562774],
[-1.01335264, -0.55329476],
[-0.02516625, 0.3408787 ]])
C = rand(10,10); C
array([[ 0.50088428, 0.93300777, 0.37201697, 0.77327375, 0.46656404,
0.62428764, 0.22893919, 0.05437433, 0.25646812, 0.61869992],
[ 0.21738864, 0.14611412, 0.6931886 , 0.01817277, 0.77878839,
0.72566348, 0.04703873, 0.93371262, 0.83055894, 0.58275793],
[ 0.4355275 , 0.64907709, 0.74873456, 0.01012651, 0.24467361,
0.2129306 , 0.55225695, 0.84802033, 0.76059712, 0.4016598 ],
[ 0.30799587, 0.27933615, 0.86267317, 0.39175961, 0.6428809 ,
0.75737427, 0.41230321, 0.56131722, 0.69304986, 0.94859853],
[ 0.62737424, 0.37229053, 0.75572847, 0.0568789 , 0.94284048,
0.97024807, 0.22325789, 0.93904313, 0.83170287, 0.65638246],
[ 0.45016252, 0.68649037, 0.71527278, 0.16762903, 0.33766686,
0.60118736, 0.34700568, 0.72236911, 0.70477416, 0.25416372],
[ 0.61660476, 0.1965179 , 0.28903584, 0.10889469, 0.76724818,
0.68422022, 0.79335408, 0.46277956, 0.91468881, 0.67903228],
[ 0.12111865, 0.59213305, 0.1991645 , 0.08751303, 0.89810622,
0.15385135, 0.90440875, 0.47300424, 0.92589573, 0.12016823],
[ 0.04863678, 0.12421563, 0.44208702, 0.52011922, 0.4823349 ,
0.27295407, 0.8477118 , 0.77363518, 0.74753611, 0.01119114],
[ 0.82594717, 0.33727314, 0.04060328, 0.28458626, 0.9967468 ,
0.18169722, 0.10745559, 0.74661605, 0.42308565, 0.52056614]])
D = around(rand(10,10)*10); D
array([[ 9., 2., 8., 3., 9., 1., 9., 9., 1., 2.],
[ 8., 5., 8., 3., 3., 7., 2., 4., 4., 8.],
[ 3., 5., 0., 6., 9., 5., 10., 3., 4., 2.],
[ 3., 9., 9., 9., 2., 1., 8., 3., 6., 1.],
[ 4., 8., 5., 5., 1., 1., 3., 1., 2., 10.],
[ 8., 9., 8., 7., 4., 7., 9., 1., 3., 6.],
[ 4., 5., 3., 0., 9., 6., 7., 6., 8., 4.],
[ 3., 6., 6., 2., 1., 7., 2., 5., 4., 1.],
[ 6., 4., 8., 9., 5., 2., 8., 9., 1., 9.],
[ 9., 8., 5., 7., 6., 6., 2., 5., 6., 2.]])
matrace(B), B.trace()
(-1, 0.50261872238441196)
matrace(D), D.trace()
(46.0, 46.0)
matrace(D.T), D.T.trace()
(46.0, 46.0)
matrace(inv(D)), inv(D).trace()
(1.2606176554219353, 1.2606176554219353)
F = array(((1,2,3),(-1,-2,-3),(2,1,0))); F
array([[ 1, 2, 3],
[-1, -2, -3],
[ 2, 1, 0]])
G = array(((1,2,3),(-1,-2,-3))); G
array([[ 1, 2, 3],
[-1, -2, -3]])
matrace(F), F.trace() ## -1 = error or result?
(-1, -1)
matrace(G), G.trace() ## -1 = error or result?
(-1, -1)
Try to use exceptions to idicate an error condition!
def matrace(A):
if A.shape[0] == A.shape[1]: # square matrix
return sum(A.diagonal())
else:
raise ValueError("Not a square matrix. Sorry.")
matrace(F), F.trace() ## -1 must is result
(-1, -1)
matrace(G), G.trace() ## error throws exception
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-17-a14741b5c239> in <module>()
----> 1 matrace(G), G.trace() ## error throws exception
<ipython-input-15-933595dad0e3> in matrace(A)
3 return sum(A.diagonal())
4 else:
----> 5 raise ValueError("Not a square matrix. Sorry.")
ValueError: Not a square matrix. Sorry.
try:
matrace(G)
except( ValueError):
print("Exception catched! Calculation of trace didn't work")
Exception catched! Calculation of trace didn't work