Numerical Methods in Earth Sciences: Finite differences



Lecturer: Heiner Igel

 merapi


The goal of the following exercises is to get you acquainted with Matlab, its options as a programming language and visualisation tool, and run/modify some of the programs that are discussed/developped in the lectures on numerical methods. Note: Matlab has excellent online documentation. Type" >> help" or >> "help command"  or  ">> demo" for more information. To edit the Matlab executable programs (runme.m files) simply type ">> edit runme" or use your favourite editor from the Linux, Unix commandline (or Windows). 


Exercise 1: Newton Cooling
Download the program cooling.m and run it with Matlab. Analyse the code and the various finite-difference approximations used. Change the time increment dt and describe the behavior of the different solutions. Refer to the lecture slides for details.


Exercise 2: The seismometer equation
Download the program seismometer.m and run it with Matlab. The program is a solution to the forced and damped oscillator descriptive of a simple mechanical seismometer system. Play around with the forcing frequency of the ground motion and the damping constant to investigate the response of the seismometer (red) to the ground motion input (blue). Refer to exercises.


Exercise 3: An ocean gyre
Download the program gyre1d.m and run it with Matlab (you also need the program csh.m). The program is a 1D solution to the diffusion-reaction-advection equation that may describe the behavior of tracers (e.g., isotopes) in the oceans (compare with the exercises). Uncomment some of the other possible solutions and investigate the numerical solutions.


Exercise 4: Acoustic wave propagation

Download the Matlab Program ac2d.m . Open Matlab in a Command Window . Try to run the model by typing >> ac2d  in the working directory
  1. Determine numerically the stability limit of the code as accurately as possible by varying eps.
  2. Extend the code by adding the option to use a 5-point difference operator (see problem 1 of exercise sheet). Compare simulations with the 3-point and 5-point operator. Is the stability limit still the same?
  3. Increase the frequency of the wavefield by varying f0. Investigate the angular dependence of the wavefield. Why does the wavefield look anisotropic. Which direction is the most accurate and why?
  4. Modify the velocity model c and observe the resulting wavefield
    • Add a low(high) velocity layer near the surface. Put the source at zs=2.
    • Add a vertical low velocity zone (fault zone) of a certain width (e.g. 10 grid points), and discuss the resulting wavefield
    • Simulate topography by setting the pressure to 0 above the surface. Use a Gaussian hill shape or a random topography.
    • etc.


Exercise 5: Relaxation vs. time-dependent solution (advanced)
We want to investigate what  approach is more appropriate to run a diffusion problem into a stationary state. The time-dependent diffusion equation is given as:
ge
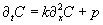k is diffusivity, C and p are space and time-dependent functions.  In the stationary state d/dt(C)=0, so
fg

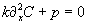a) Find an appropriate  finite-difference scheme to solve the time-dependent problem and write a Matlab program

b) Develop an appropriate relaxation scheme for the stationary problem.

Compare the solutions for k=30km2/a (a-1 Jahr). Space is defined between [0, 100km]. P ist a source function, set p=1 at x=50km, 0 else(this could be a constant temperature or concentration). Use 100 grid points in x. Find an appropriate time step for the time-dependent solution and let it run into a stationary state. Compare with the analytical solution and the solution using the relaxation algorithm.    



Exercise 6: Finite differences vs. finite elements
We want to compare the numerical solutions of the acoustic wave equation using finite differences and finite elements. Download the program femfd.m and the circular shift function csh.m and run it (>> femfd). Inspect the source code and appreciate the entirely different  approach to solving the  acoustic wave equation (by matrix inversion in the FEM case and by differencing in the FD case). We want to demonstrate the flexibility of the FEM approach by  modifying the regular grid spacing. Options are (1) to add a random perturbation to the regular grid spacing, (2) to make a sinusoidal perturbation of the grid spacing, (3) Gaussian perturbation, (4) Chebyshev collocation points. Implement one or several of those perturbations and investigate the influence on the solution.





Have fun!


HI, June 2007